Next-bit test
In cryptography and the theory of computation, the next-bit test[1] is a test against pseudo-random number generators. We say that a sequence of bits passes the next bit test for at any position  in the sequence, if an attacker knows the
in the sequence, if an attacker knows the  first bits, he cannot predict the
first bits, he cannot predict the 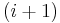 st with reasonable computational power.
st with reasonable computational power.
Contents |
Precise statement(s)
Let  be a polynomial, and
be a polynomial, and 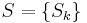 be a collection of sets such that
be a collection of sets such that 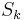 contains
contains 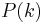 -bit long sequences. Moreover, let
-bit long sequences. Moreover, let 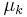 be the probability distribution of the strings in
be the probability distribution of the strings in 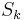 .
.
We now define the next-bit test in two different ways.
Boolean circuit formulation
A predicting collection[2] 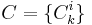 is a collection of boolean circuits, such that each circuit
is a collection of boolean circuits, such that each circuit 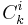 has less than
has less than 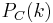 gates and exactly
gates and exactly  inputs. Let
inputs. Let 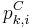 be the probability that, on input the
be the probability that, on input the  first bits of
first bits of  , a string randomly selected in
, a string randomly selected in 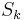 with probability
with probability 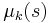 , the circuit correctly predicts
, the circuit correctly predicts 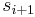 , i.e. :
, i.e. :
![p_{k,i}^C={\mathcal P} \left[ C_k(s_1\ldots s_i)=s_{i%2B1} \right | s\in S_k\text{ with probability }\mu_k(s)]](/2012-wikipedia_en_all_nopic_01_2012/I/4b24e79eda4f56c61977bcd918e8eb2f.png)
Now, we say that 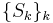 passes the next-bit test if for any predicting collection
passes the next-bit test if for any predicting collection  , any polynomial
, any polynomial  :
:
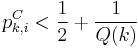
Probabilistic Turing machines
We can also define the next-bit test in terms of probabilistic Turing machines, although this definition is somewhat stronger (see Adleman's theorem). Let 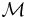 be a probabilistic Turing machine, working in polynomial time. Let
be a probabilistic Turing machine, working in polynomial time. Let 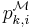 be the probability that
be the probability that 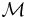 predicts the
predicts the 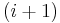 st bit correctly, i.e.
st bit correctly, i.e.
![p_{k,i}^{\mathcal M}={\mathcal P}[M(s_1\ldots s_i)=s_{i%2B1} | s\in S_k\text{ with probability }\mu_k(s)]](/2012-wikipedia_en_all_nopic_01_2012/I/8784d625b41d84ee6d4d52fa1459d99d.png)
We say that collection 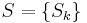 passes the next-bit test if for all polynomial
passes the next-bit test if for all polynomial  , for all but finitely many
, for all but finitely many  , for all
, for all 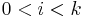 :
:
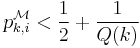
Completeness for Yao's test
The next-bit test is a particular case of Yao's test for random sequences, and passing it is therefore a necessary condition for passing Yao's test. However, it has also been shown a sufficient condition by Yao.[1]
We prove it now in the case of probabilistic Turing machine, since Adleman has already done the work of replacing randomization with non-uniformity in his theorem. The case of boolean circuits cannot be derived from this case (since it involves deciding potentially undecidable problems), but the proof of Adleman's theorem can be easily adapted to the case of non-uniform boolean circuits families.
Let 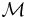 a distringuer for the probabilistic version of Yao's test, i.e. a probabilistic Turing machine, running in polynomial time, such that there is a polynomial
a distringuer for the probabilistic version of Yao's test, i.e. a probabilistic Turing machine, running in polynomial time, such that there is a polynomial  such that for infinitely many
such that for infinitely many 
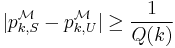
Let 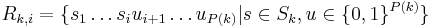 . We have :
. We have : 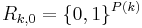 and
and 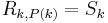 . Then, we notice that
. Then, we notice that 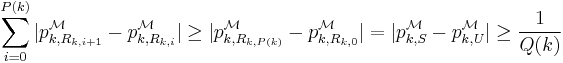 . Therefore, at least one of the
. Therefore, at least one of the 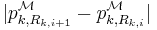 should be no smaller than
should be no smaller than 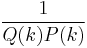 .
.
Next, we consider probability distributions 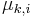 and
and 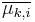 on
on 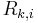 . Distribution
. Distribution 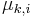 is the probability distribution of choosing the
is the probability distribution of choosing the  first bits in
first bits in 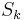 with probability given by
with probability given by 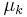 , and the
, and the 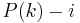 remaining bits uniformly at random. We have thus :
remaining bits uniformly at random. We have thus :
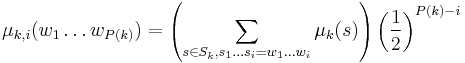
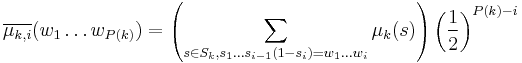
We thus have 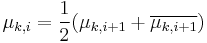 (a simple calculus trick shows this), thus distributions
(a simple calculus trick shows this), thus distributions 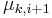 and
and 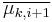 can be distinguished by
can be distinguished by  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that 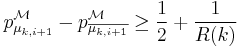 , with
, with  a polynomial.
a polynomial.
This gives us a possible construction of a Turing machine solving the next-bit test : upon receiving the  first bits of a sequence,
first bits of a sequence, 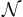 pads this input with a guess of bit
pads this input with a guess of bit 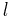 and then
and then  random bits, chosen with uniform probability. Then it runs
random bits, chosen with uniform probability. Then it runs 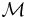 , and outputs
, and outputs 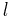 if the result is
if the result is 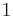 , and
, and 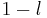 else.
else.
References
- ^ a b Andrew Chi-Chih Yao. Theory and applications of trapdoor functions. In Proceedings of the 23rd IEEE Symposium on Foundations of Computer Science, 1982.
- ^ Manuel Blum and Silvio Micali, How to generate cryptographically strong sequences of pseudo-random bits, in SIAM J. COMPUT., Vol. 13, No. 4, November 1984